이진 트리 (Binary Tree)

2진트리(Binary Tree)

2진 트리(Binary Tree)란 각각의 노드가 최대 두개의 자식 노드를 가지는 트리이다.

 

목차

1. 순회

1. 종류

1. 완전 이진 트리 구현

 

순회

비선형 자료구조인 트리의 순회에는 많은 방법이 존재한다.

• 전위순회 (Preorder)

• 중위순회 (Inorder)

• 후위순회 (Postorder)

 

전위 순회

부모 노드 - 왼쪽 자식 노드 - 오른쪽 자식 노드 순서로 순회한다.

중위 순회

왼쪽 자식 노드 - 부모 노드 - 오른쪽 자식 노드 순서로 순회한다.

후위 순회

왼쪽 자식 노드 - 오른쪽 자식 노드 - 부모노드 순서로 순회한다.

 

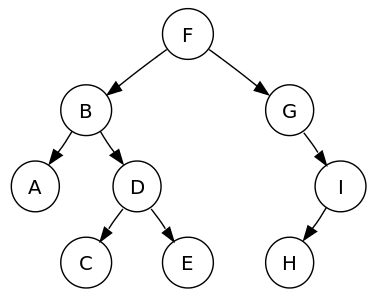
출처 : wikipedia

 

• 전위 순회 : F - B - A - D - C - E - G - I - H

• 중위 순회 : A - C - E - D - B - F - G - H - I

• 후위 순회 : A - C - E - D - B - H - I - G - F

 

순회의 구현

이진트리의 순회는 재귀로 쉽게 구현 할 수 있다.

 

• 전위순회

preorder(node){
        console.log(node.value);
        if(node.left) preorder(node.left);
        if(node.right) preorder(node.right);
}

 

• 중위순회

inorder(node){
        if(node.left) inorder(node.left);
        console.log(node.value);
        if(node.right) inorder(node.right);
}

• 후위순회

postorder(node){
        if(node.left) postorder(node.left);
        if(node.right) postorder(node.right);
        console.log(node.value);
}

 

종류

• 사향 이진트리 (Skewed Binary Tree)

• 완전 이진트리 (Complete Binary Tree)

• 포화 이진트리 (Full Binary Tree)

• 이진 탐색트리, 힙, AVL 트리 등

 

사향 이진 트리 (Skewed Binary Tree)

한쪽으로 치우친 트리구조

 

 

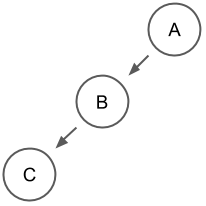
완전 이진 트리 (Complete Binary Tree)

위에서 아래로, 왼쪽에서 오른쪽으로 순서대로 채워진 트리구조, 임의의 리프노드 두개의 레벨 차가 1이하이다.

 

 

 

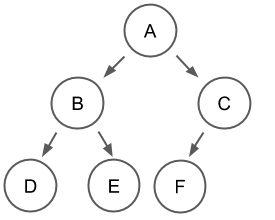
포화 이진 트리 (Full Binary Tree)

완전 이진 트리이면서 모든 리프노드의 레벨이 같은 트리구조

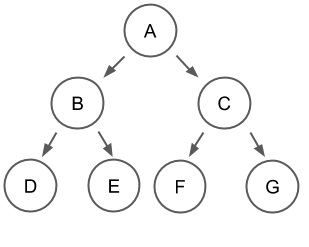
완전 이진 트리 구현

1. 참조를 이용한 방법(Linked List)

1. 배열을 이용한 방법

 

참조를 이용한 방법 (Linked List)

참조를 이용한 방법은 구현이 쉽고 이해하기 쉽지만, 배열을 이용한 방법에 비해 시간 복잡도가 높을 수 있다.

 

class Node {
    constructor(value) {
        this.value = value;
        this.left = null;
        this.right = null;
    }
}

class Tree {
    constructor() {
        this.root = null;
        this.addingQueue = [];
    }

    addNode(value) {
        const newNode = new Node(value);
        if (!this.root) return this.root = newNode;

        let current;
        if (this.addingQueue.length) {
            current = this.addingQueue.shift();
        } else {
            current = this.root;
        }
        if (!current.left){
            this.addingQueue = [];
            return current.left = newNode;
        }

        if (!current.right) {
            this.addingQueue = [];
            return current.right = newNode;
        }

        this.addingQueue.push(current.left);
        this.addingQueue.push(current.right);

        return this.addNode(value);
    }

    preorder(){
        console.log("preorder start");
        const current = this.root;
        this._preorder(current);
    }

    _preorder(node){
        console.log(node.value);
        if(node.left) this._preorder(node.left);
        if(node.right) this._preorder(node.right);
        return;
    }
    
    inorder(){
        console.log("inorder start");
        const current = this.root;
        this._inorder(current);
    }
    
    _inorder(node){
        if(node.left) this._inorder(node.left);
        console.log(node.value);
        if(node.right) this._inorder(node.right);
        return;
        
    }
    
    postorder(){
        console.log("postorder start");
        const current = this.root;
        this._postorder(current);
    }
    
    _postorder(node){
        if(node.left) this._postorder(node.left);
        if(node.right) this._postorder(node.right);
        console.log(node.value);
        return;
        
    }

}

const tree = new Tree();
const arr = ['a','b','c','d','e','f','g','h','i']

for(let val of arr){
    tree.addNode(val);
}

tree.preorder();
tree.inorder();
tree.postorder();

 

배열을 이용한 방법

배열을 이용한 방법은 직관적이지 않기 때문에 구현이 쉽지 않고 이해하기 쉽지 않지만, 시간복잡도를 줄일 수 있다.

 

class Node {
    constructor(value, index) {
        this.value = value;
        this.index = index;
        this.leftIndex = index * 2 + 1;
        this.rightIndex = index * 2 + 2;
        this.parentIndex = index - 1 < 0 ? null : (index - 1) / 2;
    }

}

class Tree {
    constructor() {
        this.contents = [];
        this.root = null;
    }

    addNode(value) {
        const index = this.contents.length;
        const newNode = new Node(value, index);
        this.contents.push(newNode);

        if (index === 0) return this.root = newNode;
        return newNode;
    }

    preorder() {
        console.log("preorder start");
        const current = this.root;
        this._preorder(current);
    }

    _preorder(node) {
        const left = this.contents[node.leftIndex];
        const right = this.contents[node.rightIndex];

        console.log(node.value);

        if (left) this._preorder(left);
        if (right) this._preorder(right);
        return;
    }

    inorder() {
        console.log("inorder start");
        const current = this.root;
        this._inorder(current);
    }

    _inorder(node) {
        const left = this.contents[node.leftIndex];
        const right = this.contents[node.rightIndex];

        if (left) this._inorder(left);
        console.log(node.value);
        if (right) this._inorder(right);
        return;

    }

    postorder() {
        console.log("postorder start");
        const current = this.root;
        this._postorder(current);
    }

    _postorder(node) {
        const left = this.contents[node.leftIndex];
        const right = this.contents[node.rightIndex];

        if (left) this._postorder(left);
        if (right) this._postorder(right);
        console.log(node.value);
        return;

    }



}


const tree = new Tree();

const arr = [1, 2, 3, 4, 5, 6, 7];

for (let val of arr) {
    tree.addNode(val);
}

tree.preorder();
tree.inorder();
tree.postorder();

참조

트리 순회
https://ko.wikipedia.org/wiki/%ED%8A%B8%EB%A6%AC_%EC%88%9C%ED%9A%8C

09-자료구조: 트리(Tree) -> 이진트리(Binary Tree) -> 이진탐색트리(Binary Search Tree)
https://m.blog.naver.com/PostView.nhn?blogId=justkukaro&logNo=220618338784&proxyReferer=https%3A%2F%2Fwww.google.com%2F

강의노트 22. 자료구조 - tree(트리), heap(힙)
https://wayhome25.github.io/cs/2017/04/19/cs-23/